This is a tale in three parts. First I’ll make a convincing claim that I am Satoshi by providing a never-seen-before, valid signature for one of their public keys. Then I’ll explain the claim’s flaws through questions and answers, and conclude with the moral of the story!

Why I am Satoshi

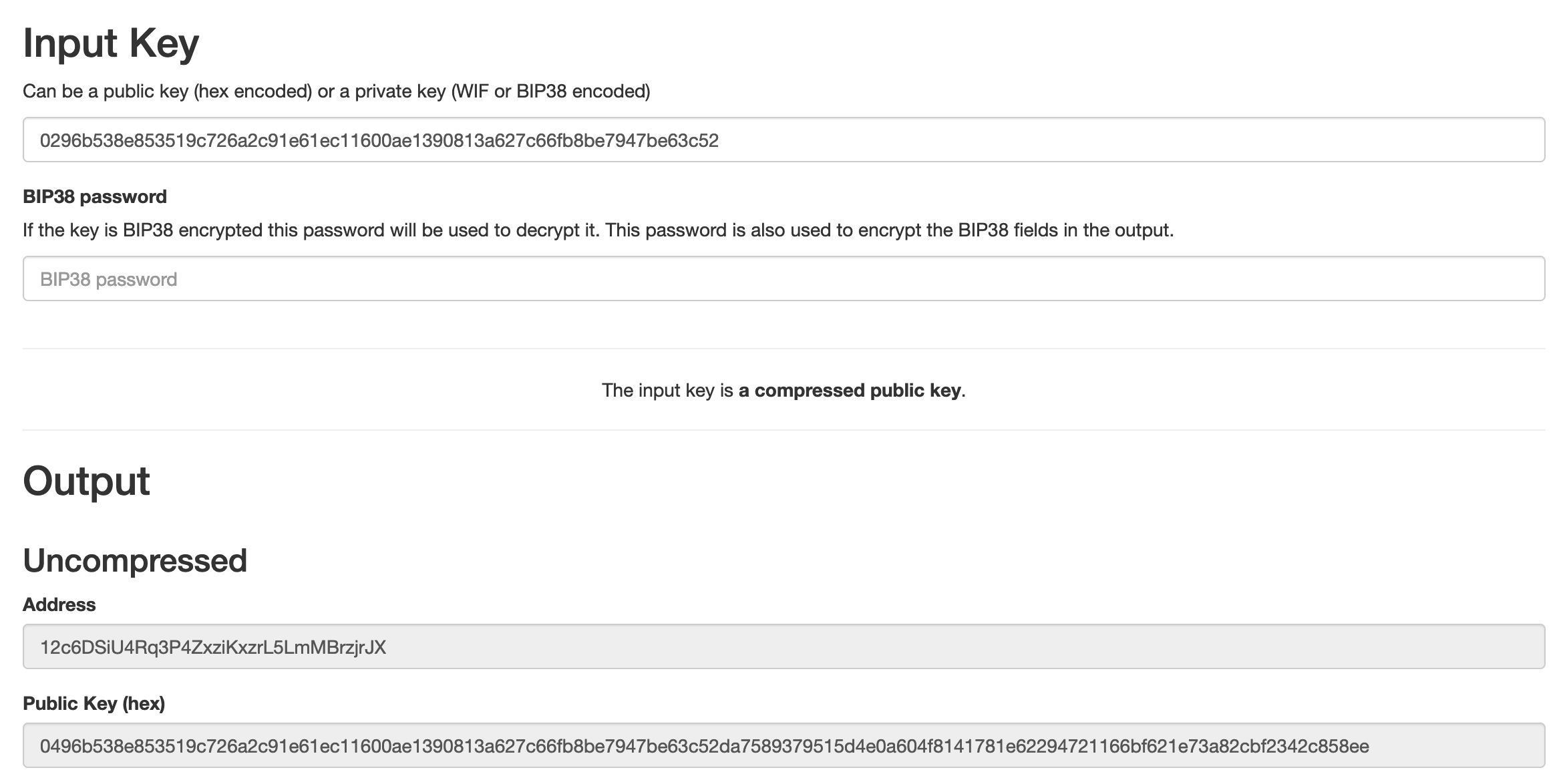
Go to any block explorer and look at the first transaction ever made on the Bitcoin network: 0e3e…2098. It sent 50BTC to the following address: 12c6DSiU4Rq3P4ZxziKxzrL5LmMBrzjrJX.

The public key associated with this address is 0296b538e853519c726a2c91e61ec11600ae1390813a627c66fb8be7947be63c52.

You can use this tool to convince yourself that it’s true:

I can produce a valid signatures

Here is a new and never-seen-before signature, valid for Satoshi’s public key:

• R: 4bb1b2164d4c82b87e4ba0bf546f0557eacc9b7e3b9c91e0318d21efc8018031
• S: 8912be5021535357e820281174b44d8d0692fd699f052fcc05aec1577b7f819e
• Hash: b6e53001048653817bea00f48000e2c90e547796300853b667746cac08e43420

Once again: I claim that the above is a valid signature for Satoshi’s public key, 0296b538e853519c726a2c91e61ec11600ae1390813a627c66fb8be7947be63c52

How can you verify this? (2 ways!)

Any cryptography library will do. Taking two popular libraries as examples:

• @noble/curves
• python-ecdsa

Verifying with @noble/curves

Here’s the source for verify.js, a Node script importing @noble/curves only:

import { secp256k1 } from '@noble/curves/secp256k1';

const signature = Buffer.from(process.argv[2], 'hex');
const message = Buffer.from(process.argv[3], 'hex');
const publicKey = Buffer.from(process.argv[4], 'hex');

console.log(
    "is valid?",
    secp256k1.verify(
        signature,
        message,
        publicKey
    )
);

And here’s how you’d run it to verify the Satohi signature above:

$ node verify.js 4bb1b2164d4c82b87e4ba0bf546f0557eacc9b7e3b9c91e0318d21efc80180318912be5021535357e820281174b44d8d0692fd699f052fcc05aec1577b7f819e b6e53001048653817bea00f48000e2c90e547796300853b667746cac08e43420 0296b538e853519c726a2c91e61ec11600ae1390813a627c66fb8be7947be63c52
is valid? true

Verifying with python-ecdsa

The Python version isn’t much longer. Below is verify.py, a Python script using python-ecdsa:

import sys
from ecdsa import curves
from ecdsa import VerifyingKey

if __name__ == "__main__":
    signature = sys.argv[1]
    digest = sys.argv[2]
    public_key = sys.argv[3]
    
    k = VerifyingKey.from_string(
        bytes.fromhex(public_key),
        curve=curves.SECP256k1
    )
    print(
        "is valid?",
        k.verify_digest(
            bytes.fromhex(signature),
            bytes.fromhex(digest)
        )
    )

Running this python script with the same Satoshi signature:

$ pip install ecdsa
$ python verify.py 4bb1b2164d4c82b87e4ba0bf546f0557eacc9b7e3b9c91e0318d21efc80180318912be5021535357e820281174b44d8d0692fd699f052fcc05aec1577b7f819e b6e53001048653817bea00f48000e2c90e547796300853b667746cac08e43420 0296b538e853519c726a2c91e61ec11600ae1390813a627c66fb8be7947be63c52
public key 0296b538e853519c726a2c91e61ec11600ae1390813a627c66fb8be7947be63c52
is valid? True

Are you convinced? Nice. Now onto part two, where we dig into what happened here.

Why I’m not Satoshi

More specifically: why is the claim above not sufficient? After all I’m able to demonstrate that I was able to present a new signature for Satoshi’s public key, and show that it’s valid!

So where’s the catch? Let the Socratic dialog begin!

“This isn’t the right public key to verify against!”

Womp. It actually is! Go back to part 1, and check this yourself, with a block explorer and the independent tool I linked.

“The signature isn’t actually valid!”

Womp womp. The two packages are picked are as legit as they come!

“The signature isn’t actually new!”

Womp, womp, womp. I even built a tool to generate Satoshi signatures on demand! Check this out: Satoshi signatures

“Hold on. Where is the private key?!…”

Warmer. Now you’re probably wondering how I’m able to produce signatures without a private key. If you look at the source code for it (specifically, the makeSignature function), there’s indeed no sign of the private key! How can it be?

“The hash is constructed artificially!”

Bingo! You got it. This script implements what’s known as an existential forgery attack. We can carefully construct a hash and the associated signature such that they’re considered valid under the verification procedure.

This comment runs through the math behind it. This demo app implements it, because I needed to convince myself that it works for real!

“So you didn’t really produce a message signature did you?”

You’re fast! That’s exactly it. The constructed hashes are meaningless, and I’d be hard-pressed to find a pre-image for any of them: hash functions are by definition pre-image resistant!

In other words I shouldn’t be able to find a message such that hash(message) = H for any given constructed hash.

“Nice. So it’s all good? ECDSA isn’t broken?”

All good indeed, as long as hashing is part of the verification procedure! Verifiers, never forget: hash before verifying!

“What about other signature schemes?”

Good question. All signature schemes which use hash functions as Random Oracles are vulnerable to this. I focused on ECDSA to demonstrate a concrete forgery. Schnorr, RSA, ElGamal, and probably many more digital signature schemes out there are vulnerable: if hashing isn’t performed during signature verification, the Random Oracle assumption flies out the window!

Moral of the story

We’ve seen that verifying a signature against a digest (without computing it yourself) breaks a fundamental ECDSA assumption. Specifically, it breaks the Random Oracle assumption. The output of a hash function is assumed to be unpredictable; by constructing hash values artificially we broke this assumption, and ECDSA verification fell apart as a result.

If you’re working with cryptography libraries, it’s easy to make this mistake by accident and allow verification logic to accept arbitrary digests as input:

• @noble/curves’s default behavior for verify is to avoid hashing the message!
• python-ecdsa is one-step better: verify hashes the message. However verify_digest doesn’t, and sound just as legitimate!

This is not talked about widely enough. I learned about this “gotcha” a few weeks ago after many years working in crypto. The trigger? A comment in the excellent RustCrypto/traits crate piqued my interest:

/// # ⚠️ Security Warning
///
/// If `prehash` is something other than the output of a cryptographically
/// secure hash function, an attacker can potentially forge signatures by
/// solving a system of linear equations.

I asked for clarifications with a new Github issue, the maintainer replied within a couple of hours (❤️), and I learned something valuable that day. Now that you’ve read this, I hope the same is true for you!

Moral of the story: never verify without hashing first.