Lightning Network: 7 "Aha!" moments to make it click

I recently finished reading Mastering the Lighning Network (Amazon link, Github link). This book does a great job explaining the design of the Lightning Network and the details of the protocol. I had a few “Aha!” moments while reading it and I’d like to share them with you!

To get the most out of this note, no prior knowledge about the Lightning Network is required, but a basic understanding of Bitcoin’s UTXO model and scripting capability is.

Aha! A true peer-to-peer network!

The Bitcoin network is famously “A Peer-to-Peer Electronic Cash System” (this is in the title of the Bitcoin whitepaper!). However, participants are split in practice:

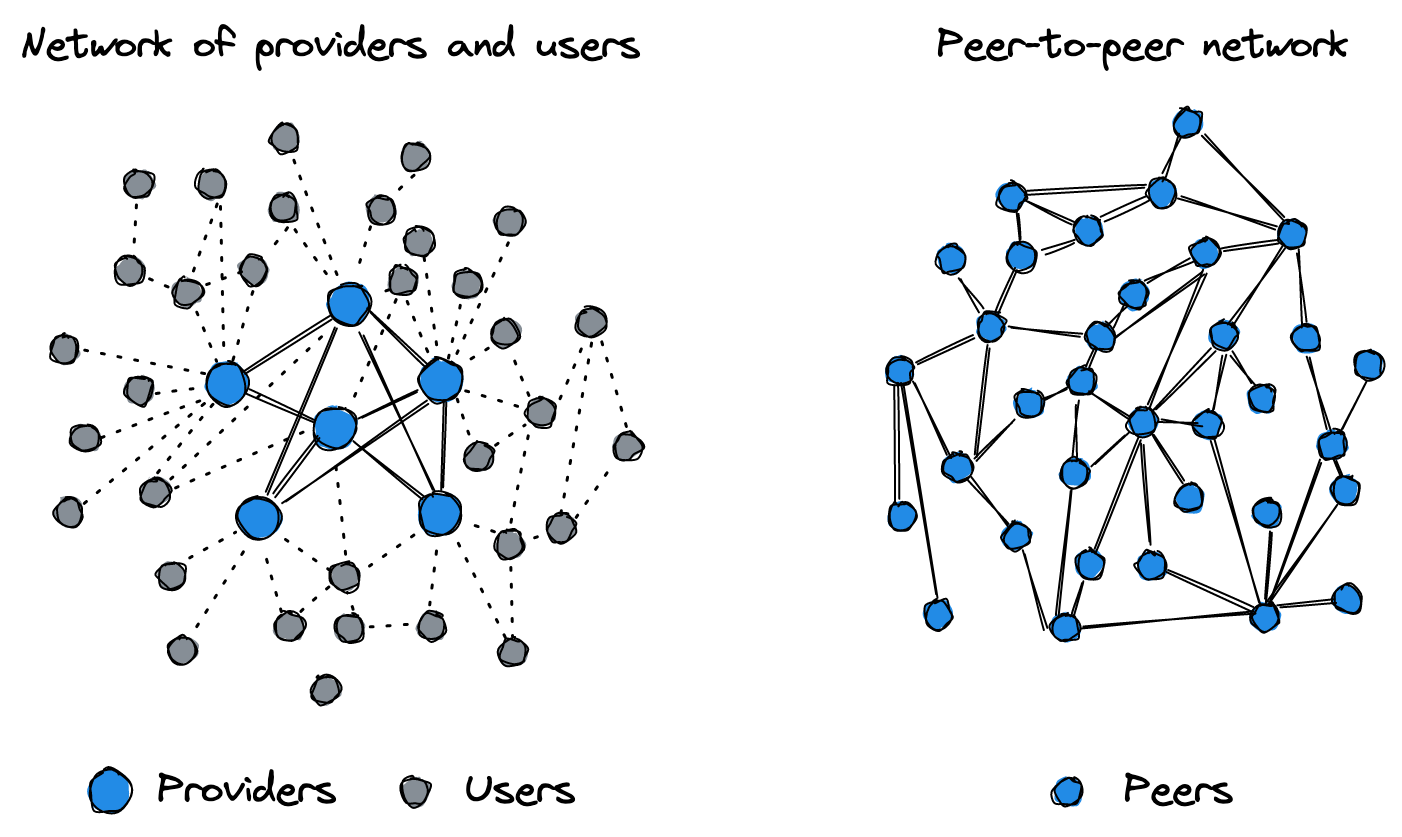
Network types

The Lightning Network, however, is only composed of peer-to-peer relationships called channels. Channels are the pathways of the network, through which payments travel. All participants must open at least one channel to another participant to send and receive payments. The network is a big, amorphous graph of participants connected to each other with channels, all on the same level.

Aha! Transfers are “lightning” fast because…there are no transfers!

Surprise: the protocol outlined in the Lightning Network standards (“BOLTS”) does not define value transfer. At its core, the Lightning Network is a protocol for two participants to pool funds together and make commitments to splitting this fund pool. This split evolves over time, enabling “transfers”. For example, say I want to send you 0.5 BTC through a channel you and I have opened. At the moment there is 1 BTC on my side and 2 BTC on yours. If we both agree to split 0.5 BTC / 2.5 BTC instead of currently 1 BTC / 2 BTC, the transfer is done!

It’s easy to understand why these kinds of transfers are wicked fast: they’re not actually happening. Only commitments are exchanged between participants.

Aha! Funds are pooled via multisig, with pre-signed transactions as insurance!

You’re probably wondering how commitments actually work. It seems magic. Participants cannot trust each other, making this a hard problem. The Lightning Network solves this by pooling funds through multisig, and committing with pre-signed Bitcoin transactions.

Pooling. Pooling funds is done through a Bitcoin primitive you probably know already: multisig. Opening a Lightning channel is equivalent to funding a “2-out-of-2” multisig address. If you and I deposit funds into a 2-out-of-2 address, neither of us can unilateraly move these funds. That’s good but: how can I get my money back if you lose your key or go offline? What if you never agree to sign a transaction even when I’m just taking my fair share? This is where pre-signed Bitcoin transactions (also called “commitment transactions”) come in.

Committing. Agreeing on who owns what share of the fund pool is done via pre-signed offline Bitcoin transactions. These transactions are called “commitment transactions”, or “commitments” for short. They spend funds out of the multisig address and split them across the two channel partners. They provide an important guarantee: in case things go wrong, the commitment transactions can be broadcast and funds are sent out of the multisig address, back to the channel partners, according to the agreed upon split. Therefore, it’s crucial to put this guarantee in place before sending funds to the multisig address! (if you’re wondering how that’s possible, the next section on SegWit has answers for you!)

How are commitments put in place? Well, here are the messages exchanged to open a Lightning channel:

When a channel is open, 100% of the funds are allocated to the channel opener. To update the channel balance old commitments are revoked, and a new one established.

Aha! SegWit enables offline chaining of signed transactions!

SegWit solves the transaction malleability problem. Before SegWit signatures (aka “witnesses”) were part of the data hashed to produce transaction identifiers. This meant that the transaction hash (or ID) could change if the signature bytes changed. Given signatures aren’t deterministic (signers can pick different nonces, observers can also flip the “s” value or play with DER encoding to get the same signature encoded with different bytes), it was not safe to expect that a signed, off-chain transaction would keep its ID. The only safe way to get a reliable transaction ID was to broadcast it on-chain. As a result chaining signed transactions without broadcasting them was risky.

SegWit solves this by excluding (or, segregating) signatures (or, witnesses) from the data hashed to produce a transaction ID. As a result, a change in the signature won’t change the transaction ID. This is why it’s safe to rely on this ID to construct another transaction using it, even if it’s not broadcast on-chain.

This is fundamental for the Lightning network since commitment transactions (remember, they’re our “insurance”) have to be signed before funding transactions are broadcast, yet commitment transactions need the funding transaction ID to be constructed. In other words, the Lightning Network would not be able to function without SegWit and offline transaction chaining.

Aha! Bitcoin script and game theory to harden commitment outputs!

To update the channel balances, old commitments need to be revoked and a new one established. This is done with a simple exchange of messages:

Commitment transactions are sophisticated, to prevent cheating. The idea is that if I cheat by broadcasting an old commitment, you should have some time to react and punish me. In practice this is implemented with revocation secrets: when revealed they let the other party redeem a “punishment” output, taking the other party’s share. That’s the financial incentive not to broadcast old commitments.

In order to implement punishment, commitments are non-symmetrical. The “punishment” outputs have different amounts and beneficiaries: you can punish me and claim my share if I broadcast an old commitment of mine to you, and I can punish you and take your share if you broadcast an old commitment of yours to me.

To allow for cheating detection and enforcement, commitments output are delayed so that the party crafting them is forced to wait for a window of time to get their fair share. This is to ensure the other party has time to detect cheating and use their revocation secret if they so choose. The time delay is not dictated by the protocol: it is agreed upon when the channel is open (to_self_delay in open_channel)

To illustrate this, let’s take a concrete example. If A and B have a channel opened (split with 0.5 BTC for A, and 2.5 BTC for B), here are the commitment transactions on each side:

Commitment transactions

This looks complicated but the Bitcoin script to implement this is surprisingly simple. Below is the Bitcoin script for the “either/or” fork for A’s commitment to B:

OP_IF
    # revocation secret can spend the funds immediately if A cheats
    revocation_pubkey
OP_ELSE
    # This Bitcoin OP is defined
    # in BIP 112: https://github.com/bitcoin/bips/blob/master/bip-0112.mediawiki
    # It ensures the current output can't be spent before time_delay
    time_delay OP_CHECKSEQUENCE_VERIFY OP_DROP

    # If the line above succeeds (gets off the stack with `OP_DROP`),
    # public_key_for_A is able to spend the funds.
    # This only happens after a delay because of OP_CHECKSEQUENCE_VERIFY
    public_key_for_A
OP_ENDIF
# Checks signature for either revocation_pubkey or public_key_for_A
OP_CHECKSIG

There you have it, game theory and Bitcoin primitives coming together in this commitment transaction output!

Now let’s dive one layer deeper: how do revocation secrets work exactly? Remember that revocation secrets are powerful, you can claim my portion of the channel balance with it! How are they generated and how do they “revoke” commitments exactly?

Aha! Revoking a commitment is done by revealing a secret!

Revocation secret derivation is explained precisely in BOLT#3. However the technical nature of the spec masks the cleverness of its design. Let’s walk through it together!

Warning: this requires some knowledge of elliptic curve cryptography.

Click/Tap for a quick primer. Here are the important concepts to grasp:
  • What are elliptic curves?
    Short version: they're curves with the equation: y2 = x3 + ax + b. Instead of using real numbers, ECC computes all operations modulo a large prime number P
  • What is point multiplication?
    Short version: take two points on an alliptic curve, find the intersection with the elliptic curve, then negate the y coordinate to obtain the "sum" point. Sum a point P with itself x times and you have point multiplication: x*P!
  • How do public and private keys relate to elliptic curve points
    Short version: private keys are just big integers. Public keys are points on the elliptic curve. A public key or point is obtained by point multiplication: pubkey = n*G, where n is the private key and G is the generator of the curve; G is arbitrarily chosen

    • If you want more details on ECC with awesome visuals, I highly recommend reading The Animated Elliptic Curve.

    Back to the lightning network and revocation secrets!

If two parties (let’s call them “A” and “B”) open a channel, they exchange two (public) elliptic curve points as part of the flow: revocation_basepoint and per_commitment_point. Revocation public keys (revocation_pubkey) are composed from these two points:

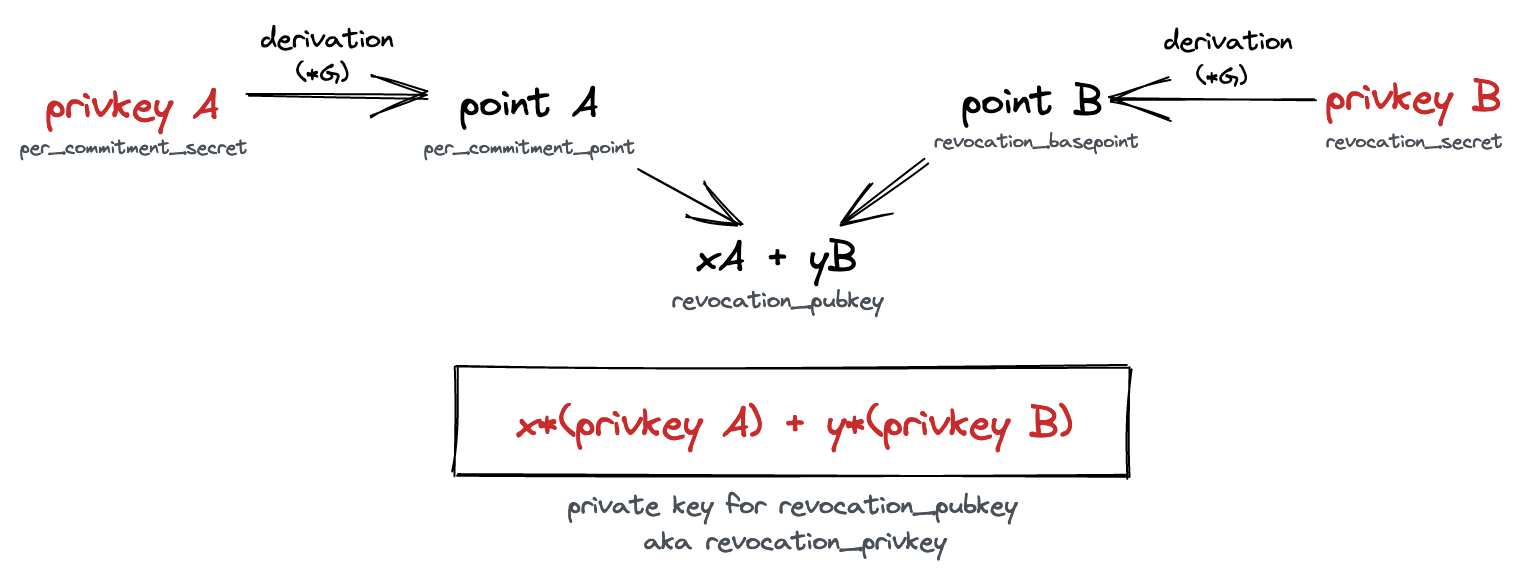
ECC trick

To make the shared point deterministic, the Lightning Network picks x and y based on values known to both parties:

revocation_pubkey = 
    revocation_basepoint
      * sha256(revocation_basepoint || per_commitment_point)
  + per_commitment_point
      * sha256(per_commitment_point || revocation_basepoint)

(In the above, || represents byte concatenation and * is ECC point multiplication)

The associated private key is given by:

revocation_privkey = 
    revocation_secret
        * sha256(revocation_basepoint || per_commitment_point)
  + per_commitment_secret
        * sha256(per_commitment_point || revocation_basepoint)

To convince yourself that this works, multiply the above expression by G and you’ll find that revocation_privkey * G results in revocation_pubkey.

Click/Tap to reveal proof 
G * revocation_privkey
= G * (
    revocation_secret
        * sha256(revocation_basepoint || per_commitment_point)
    + per_commitment_secret
        * sha256(per_commitment_point || revocation_basepoint)
  )
= G * revocation_secret
  ^-------------------^ this is revocation_basepoint!
        * sha256(revocation_basepoint || per_commitment_point)
  + G * per_commitment_secret 
  ^-------------------------^ this is per_commitment_point!
      * sha256(per_commitment_point || revocation_basepoint)
= revocation_basepoint
      * sha256(revocation_basepoint || per_commitment_point)
  + per_commitment_point
      * sha256(per_commitment_point || revocation_basepoint)
= revocation_pubkey (Q.E.D.)

revocation_pubkey can be computed by anyone since it’s composed of 2 public points. The interesting piece is the revocation_privkey, composed of two secrets spread across channel partners: revocation_secret and per_commitment_secret.

It turns out “revoking” a commitment is the act of revealing its per-commitment secret. The reveal is done with a field named per_commitment_secret in the revoke_and_ack message. This message also contains next_per_commitment_point such that the other party can compute the next revocation_pubkey and use it to craft the next commitment transaction. To make this more concrete, let’s illustrate this with our 2 channel partners, A and B:

Note: the above only describes how A creates commitments for B. When B wants to create commitments for A, it uses its own revocation_basepoint and A's series of per_commitment_point values.

Now it should be clear why commitment transactions never change, yet they’re “revoked”: when the per_commitment_secret for a given commitment is revealed, the other party can suddently compute the associated revocation_privkey and redeem the commitment’s “punishment” output if it was ever broadcast on-chain. This strong financial incentive is enough to keep old commitment transactions offline for good.

Aha! Multi-hop, atomic payments with HTLCs!

We’ve seen how the Lightning Network enables peer-to-peer payments. Now let’s move to indirect or “multi-hop” payments. If A has a channel open with B, and B has a channel opened with C, can A pay C?

Yes it can! Provided that there is a route with enough capacity from A to C, not only can A pay C, it can do so atomically. Either all legs of the payment (e.g. A->B, B->C) succeed, or all legs fail. This is possible at scale, even with 10, 15, or 20+ intermediary nodes. If you’re used to the traditional financial system where intermediaries cause hard-to-debug failures and long settlement delays…isn’t this mind-blowing?

The Lightning Network does this with Hash-Time-Lock-Contracts (“HTLCs”). These contracts are “just” valid Bitcoin scripts. The basic premise is that an HTLC is a contract between 2 parties (1 issuer, 1 recipient), and it enforces the following:

Hence the name “HTLC”, HTLC contracts are Hash-locked contract from the point-of-view of the recipient, or Time-locked contract from the point-of-view of the issuer.

How are HTLCs helping with instant, atomic payments? Here’s how a payment from A to B to C happens in practice:
(note: if you’re wondering why “B” was picked as an intermediary, we’ll see later that path discovery isn’t explicitly part of the BOLT specs! Another interesting aspect of the Lightning Network design)

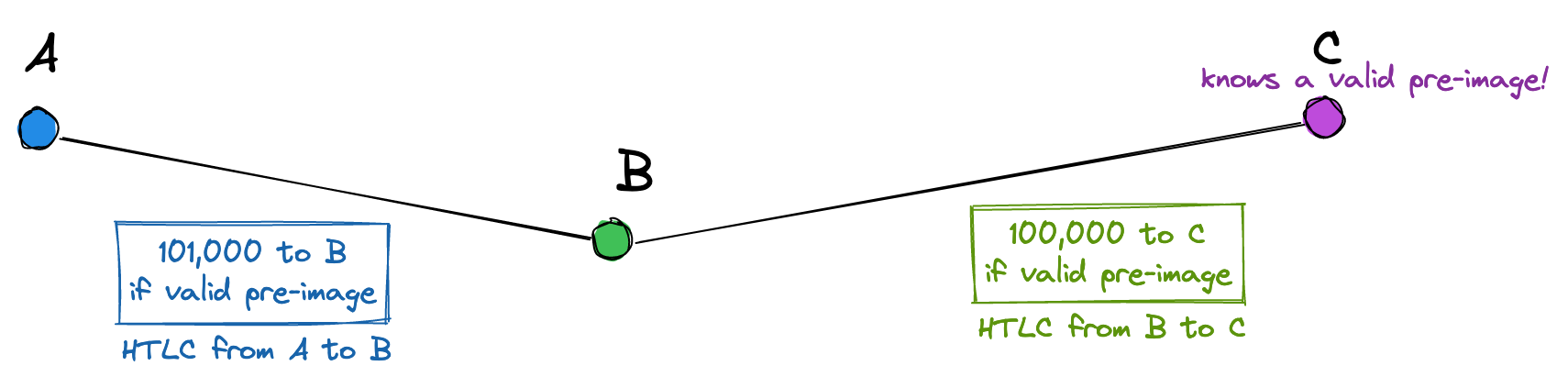
HTLC diagram: A-to-B-to-C

To redeem the HTLC, C can broadcast a transaction containing a valid pre-image. Doing this will reveal the previously secret pre-image because it’s publicly on-chain! The public reveal of the pre-image makes all HTLCs spendable by their recipients. In our example, B can now unlock the HTLC offered by A and redeem 101,000 satoshis.

This is how atomic payments are enabled: regardless of the number of intermediaries, either all HTLCs become spendable when the pre-image is publicly revealed, or none of them do.

In practice broadcasting on the Bitcoin network isn’t efficient because it incurs fees. Instead, C can send the pre-image to B, thereby prooving it could redeem the HTLC if it wanted (by going on-chain). This is enough for B to get comfortable and update the (B,C) channel balance, sending 100,000 satoshis to C.

Once B has updated the (B,C) channel balance, B can send the pre-image to A. For the same reason, A prefers to settle the HTLC off-chain and send 101,000 satoshis to B through the (A,B) channel.

For the curious reader: what's the incentive not to broadcast HTLCs on-chain after off-chain settlement is done? You may have noticed an incentive problem in the previous example: why would C not broadcast the HTLC on-chain after the channel balance is updated? After all, C has the pre-image so why not take the money twice? Once from the off-chain settlement through B's balance update, the second on-chain with the HTLC broadcast!

To fix this, the Lightning Network incorporates HTLCs into commitment transactions. In other words, B doesn’t simply send an HTLC to C. B and C actually exchange commitment transactions which include the HTLC as an extra output.

Specifically, the commitment transaction from B to C has the following outputs:

  • output to B for B’s balance minus 100,000 satoshis (delayed)
  • output to C for C’s balance (immediate)
  • output to C for B’s balance minus 100,000 satoshis (immediate with revocation key)
  • output to HTLC for 100,000 satoshis

And the commitment transaction from C to B has the following outputs:

  • output to C for C’s balance (delayed)
  • output to B for B’s balance - 100,000 satoshis (delayed)
  • output to B for C’s balance (immediate with revocation key)
  • output to HTLC for 100,000 satoshis

When C reveals the pre-image to B and B updates the channel balance with a new commitment, C has to send B the revocation key to revoke the previous commitment. This means that C can’t “double claim” the HTLC: once it’s settled off-chain, the corresponding commitment becomes obsolete. B can punish C with the revocation key if C decides to broadcast it on-chain!

Bonus: Significance of Taproot upgrade and Schnorr signatures

I’ve never connected Schnorr signatures with the Lightnint Network before. The relationship is that Schnorr signatures unlock Point Time-Locked Contracts (PTLCs). PTLCs are “Bitcoin scripts that allows a conditional spend either on the presentation of a secret or after a certain blockheight has passed, similar to an HTLC. Unlike HTLCs, PTLCs do not depend on a preimage of a hash function but rather on the private key from an elliptic curve point. The security assumption is thus based on the discrete logarithm. PTLCs are not yet implemented on the Lightning Network” (taken from the Mastering the Lightning Network’s glossary)

Bonus: Choosing NOT to design payment routing

Designing is making choices. It’s also choosing NOT to make a choice, to leave room for experimentation and innovation within the protocol boundary.

I was a bit shocked to learn that there is no standard on how to route payments in lightning. The probing for channel balances happens independently, through trial and error. Some papers have been written on how to do this independently. There’s also, in the same category, innovation on how to manage channel liquidity. For example: Loop.

This is how lightning “scales”. The protocol itself doesn’t mandate anything, actors within the lightning community are coming up with bottom-up solutions like these, getting better and better over time.

Bonus: No networking needed!

Then I realized: opening payment channels, evolving commitments, and closing channels can all be done by exchanging messages on USB drives or paper, fully offline. These messages do not have to follow BOLT standards as long as the structure of the commitment transactions is kept intact (validity of transactions on-chain is key to enforcing incentives and preventing cheating).

Nothing mandates a “network” for pure peer-to-peer payment to work. The design is extremely resilient: no privileged node assumption (all nodes are participants, all participants are nodes!), no speed or hard protocol requirement for message exchange, and no trust assumptions even for direct peers. Thanks to cryptography and game theory the only real assumption in the Lightning Network is reliable access to the Bitcoin Network, to detect and punish cheaters.

This makes the design of the Lightning Network applicable broadly:

Conclusion

If you’ve made it this far, thank you for reading. We’ve covered quite a lot of ground and have seen that:

I highly recommend reading the full version of Mastering the Lighning Network (Amazon link, Github link) if you’re looking to learn more about the Lightning Network. The design principles behind it are worth dissecting. I hope you’ll get as much satisfaction as I did while diving in!

Thanks to Rob S. and Alex M. for their valuable feedback on previous versions of this text.