Hacking Cryptography is a book I pre-ordered in 2023. A physical copy was shipped to me in March earlier this year, and I finished reading it over the summer.

I highly recommend picking up a copy if you work with cryptographic systems or concepts. I didn’t expect to learn much because I’ve read a few books on cryptography already (Cryptography Engineering, Serious Cryptography, Real-World Cryptography), but this book made a few things “click” for me. Probably because some things only truly click after you’ve seen them a few times, from different angles.

I think this book’s “angle” has something to offer to everyone. I was impressed by the fearless “end-to-end” approach: each chapter explains important concepts and goes on to show a real exploit, implemented fully (in Golang, a language that is a bit verbose but very easy to read). It arms you with knowledge (and code!) that can be used to exploit real-world systems. Usually, authors shy away from showing full exploits or from the details, watering down the explanation for educational purposes. Not here! I love the unapologetic stance: broken crypto implementations laid bare and exploited, chapter after chapter. It’s sitting at the edge of “white hat” and “black hat” material.

Chapters are structured with concept explainers first (useful to jog your memory if you’ve seen these before, or lay down the foundations if you haven’t), then exploits. After a few chapters you start thinking before the exploit comes, as you’re reading the concepts: “what could go wrong”? “What will go wrong this time around”? Below are some moments of clarity which feel valuable enough to write about.

Types of entropy sources

Have you ever wondered where “true” entropy comes from and how it can be digitized? Me neither—but this book answered that question anyway. I’ve used hardware TRNGs (typically USB-based) for key ceremonies but never researched how they work. The book explains this in detail.

True Random Number Generators (TRNGs) sample physical phenomena which must be random by nature. A well-known example of a “true” random phenomenon is radioactive decay: each atom has a random probability to decay associated with it, and radioactive decay for a large group of atoms follows a well-known exponential decay curve. Unfortunately radioactive decay is expensive to sample and use safely, hence hard to produce digital entropy from.

Other known (but flawed!) sources of entropy:

• Atmospheric noise is a cheap source of entropy because radio receivers are easy to build. Unfortunately they’re easy to fool: an attacker can influence the output with electromagnetic interference.
• Measuring CPU clock drift and using that as a source of entropy is also cheap but unfortunately that’s not trivial to use safely because attackers can influence or predict the output easily.
• The avalanche or Zener effect in diodes is a commonly used method because it’s cheap, but is subject to interference and doesn’t have a proper underlying physical model to assess the health of the TRNG hardware. There are large variations from device to device, and manufacturers do not build diodes with this use case in mind. Quite the opposite: in the context of normal operations, the avalanche effect is undesirable, and manufacturers work to reduce or eliminate it.

The book concludes this chapter by talking about MEM (Modular Entropy Multiplication), a method invented in the late 1990s. It works by amplifying thermal noise based on simple rules. The voltage has a target range (`V_{min}`, `V_{max}`), and the TRNG circuit doubles it if less than half the target range, or adds `V-V_{max}` if more than half. If V exceeds `V_{max}`, it wraps around to `V_{min}`. This method is resistant to electromagnetic interference, and comes with a physical model for health checks. Beautiful, simple, open-source hardware TRNG design. See the Infinite No-ise TRNG design and the associated REDOUBLER.

Randomness extractors

Something I didn’t know: randomness from natural sources is generally not high-entropy enough. This was new to me — and fascinating to learn. The book mentions that randomness extractors have to be used on top of TRNGs. Another interesting takeaway: randomness extractors can be remarkably simple.

The example given in the book is the following algorithm: if two successive bits (of a random input stream) match, generate no output, and if they’re different, output the first bit only. The output stream will be “denser” than the input bit stream, hence higher in entropy.

Measuring entropy requires a physical model

Entropy is a measure of randomness. In cryptography, randomness is fundamental. Thus, if you work on very sensitive cryptography (offline key generation ceremonies are a perfect example) you’ll want to use a TRNG. But how do you measure whether what you get out is “random enough”? How do you know when your device is too old or starts breaking down?

The concept that was missing for me is the concept of measurement against a physical model. A good TRNG will have theoretical foundations for why the physical phenomenon it uses is random, and the model should be able to predict the rate of entropy. The author frames this as a “health check” for TRNGs: because the physical world is messy and TRNGs are physical devices, it’s crucial to know when your TRNG starts malfunctioning. A physical model provides a baseline for measuring entropy — without it, you can’t know when a TRNG starts to fail.

Another interesting fact is that not all TRNGs have an underlying physical model, hence they should be avoided for high-security use cases. For example: TRNGs based on the Zener effect in diodes, or noise in ring oscillators, have no underlying physical models for entropy. Radioactive decay, or MEM-based TRNGs do.

CSPRNGs vs. PRNGs

I’ve always known that some random number generators are better than others. If you want strong random numbers in Golang for example, never use math/rand, always use crypto/rand. But why? My prior mental model (loosely) was that math/rand is fast but repeats a sequence of “random-looking” bytes, whereas crypto/rand uses hardware randomness and therefore produces “truly random” byte sequences. I was wrong on multiple counts!

First, a bit of definition: to be cryptographically secure (and be a CSPRNG), a PRNG should satisfy the following properties:

• An attacker should not be able to look at the output values and deduce that they came from a PRNG (as opposed to some random noise).
• An attacker should not be able to guess past values by looking at current (and future) output values. This is referred to as forward secrecy.
• An attacker should not be able to guess future values by looking at past output values. This is referred to as backward secrecy.

A useful example of a PRNG that is not cryptographically secure is the Linear Congruential Generator (LCG). Output values (X) are generated from a seed with the formula:

`X_{n+1} = (aX_n + c) mod m`

(m is the modulus, a is the multiplier, c is the increment)

The book goes on to show the weakness: it’s possible to recover m, a, and c by observing a series of output values. All it takes is a bit of linear algebra:

• The modulus m can be guessed by looking at GCD of “zeros” (numbers which are equal to 0 modulo m by construction). These “zeros” are computed by looking at differences of output numbers from the LCG we want to attack. It takes a good amount of output numbers to “crack” the modulus (~1000 observations.)
• With the modulus in hand, recovering a and c is trivial. a can be recovered by looking at the difference between 2 output values and computing an inverse modulo m, and recovering c is a simple multiplication and subtraction from there.

If you’re curious about the details, check out ch02/lcg/go/exploit_lcg.

Another insecure PRNG is described and exploited in the book: MT19937 (Mersenne-Twister). It’s a very interesting exploit because MT19937 is still the default PRNG in Ruby and Python. The exploit shows concrete code to clone an existing MT19937 and predict future values from observing a few output values. See the code here, it’s less than 50 lines total and shows, rather than tells, how insecure default PRNGs can be.

So, looking back at my initial mental model: where was I wrong?

• “Insecure” PRNGs do not repeat themselves predictably: they’re generally seeded with TRNGs. While they do repeat themselves (after a known “period”), the sequence itself is random every time the PRNG is initialized, because the seed is different every time. The reason they’re insecure isn’t the repetition, it’s the construction of the PRNG itself!
• CSPRNGs are seeded the same way as “insecure” PRNGs are, with TRNGs.
• CSPRNGs have finite periods, just like “insecure” PRNGs.
• The line between PRNG and CSPRNG isn’t black and white. It depends on how well the PRNG preserves forward and backward secrecy. Essentially, how securely it manages its internal state and next-value computation. If you can reverse them and recover a PRNG’s internal state, the CSPRNG is not cryptographically secure anymore: attackers can guess the following “random” values.

DUAL_EC_BG exploit

The DUAL_EC_BG exploit is one that I’ve heard about many times in security and cryptography contexts to explain why the NSA cannot be trusted with cryptographic standards (for a good summary of everything that has happened over the years, look no further than this DJB blog post).

Before reading this book, my understanding of the DUAL_EC_BG exploit was that there was a secret that only the NSA knew which could be used as a trapdoor, but I didn’t know the specifics and I never bothered to look into it more deeply. Embarrassingly, I also didn’t know that DUAL_EC_BG was a random number generator. I kind of assumed it was an encryption scheme? Unsure why. Turns out: “BG” stands for “Bit Generator”, and DUAL_EC_BG was one of the NIST-recommended CSPRNGs.

This exploit is fascinating for a few reasons:

• The cryptographic design of DUAL_EC_BG is solid, based on elliptic curve operations.
• The choice of the constants is where the problem lies: the backdoor is in the constant itself.
• There is no way to prove that the constant is backdoor’d unless you know the backdoor. Genius.

The design of DUAL_EC_BG is elegant because it’s simple:

• a seed is used as the RNG state (treated as a big number n).
• to generate random bytes, perform the scalar multiplication of a well-known, constant point Q: nQ, then take the first 30 bytes of its x coordinate. These are your random output bytes.
• once the bytes are generated for a given n, the state progresses: the next big number (n+1) is the x coordinate of nP, where P is another well-known and constant point.

This looks secure on paper because both “next state” and “get random output” functions rely on elliptic curve point multiplication operations, which are hard to reverse. The exploit lies in the selection of P and Q: if these constants are related to each other such that P is dQ (where d is the “secret” only known to the NSA), then the NSA can predict the “next” value by observing output values alone:

• Remember the output values are the first 30 bytes of the x coordinate of nQ. Recovering the “output point” nQ from these 30 bytes alone requires trying all values for the 2 missing bytes (from 0x0000 to 0xFFFF, ~65k values), and see which full x coordinate yields a point that lands on the underlying cryptographic curve.
• Once nQ, the output point, is recovered, multiply it by d (the hidden secret) and take the x coordinate of the resulting point to get the next state (“next state point” = nP = n*(dQ) = d*(nQ) = “d times the recovered output point!")
• And once you have the state n of the RNG, it’s trivial to predict the next random values: compute nQ and take the first 30 bytes of the x coordinate to get the next random bytes, then compute the next state, then the next random bytes, and so on. The RNG is successfully cloned.

There you have it — a CSPRNG that isn’t really “CS” if you believe the constants are backdoor’d.

Stream ciphers

What’s notable here is how the book introduces stream ciphers: they’re introduced as a clever solution to the limitation of One-Time Pads (OTPs), which is the only proven “perfectly secure” encryption scheme.

The explanation goes like this:

• OTPs require a key stream as long as the data being encrypted.
• Sharing a large amount of key stream is inconvenient and gets impossible as plaintext size grows (video files: GBs of data to encrypt; disk encryption: TBs of data!)
• The solution: share a single (short) seed, and use a CSPRNG to deterministically generate the same keystream during encryption (on the sender side) and decryption (on the receiver side)

As a reminder:

• Encryption: plaintext XOR keystream => ciphertext
• Decryption: ciphertext XOR keystream => plaintext

I thought this was a neat way to give intuition on why stream ciphers are designed this way; something clicked for me.

Cracking WEP passwords by exploiting RC4 bias

RC4 is a popular stream cipher that was used by the first Wi-Fi security standard (WEP). Attackers can recover the Wi-Fi password by snooping on encrypted communications between genuine participants and then using the statistical biases in RC4 to crack the Wi-Fi network’s password.

The attack is tricky and it’d be too long to explain it fully, but it’s done very well in the book. At a high-level, the Fluhrer, Mantin, and Shamir (FMS) attack revealed a subtle bias in the RC4 key-scheduling algorithm. More specifically: if the first and second bytes of the RC4 seed are L and 255, respectively, then the Lth index of the seed is statistically more likely to appear in certain places in the resulting keystream.

In WEP, RC4 is used in the following way:

• User knows a password (fixed)
• To seed RC4 and encrypt packets, users use IV || password as a seed, where IV is an Initialization Vector made of 3 random bytes. Each packet has its own IV.

The attack is statistical and targets one byte of the password at a time: if an IV (3-byte value) is in the form (L,255,X) (where X is any value) then it’s a vulnerable IV: the resulting keystream will leak data about the Lth byte of the RC4 seed (=IV || password). By looking for IVs matching (3,255,X) one can statistically guess the first byte of the password, IVs matching (4,255,X) leak the second byte, (5,255,X) the third, and so on.

This is the first time I’ve understood why WEP is insecure on a deep level.

Confusion vs. diffusion

First time I’ve heard about these two concepts in the context of stream and block ciphers. The book states:

Confusion hides the relation between plaintext and ciphertext. Diffusion distributes the effect of each plaintext byte over many ciphertext bytes.

I thought that was a neat way to summarize the essential difference between stream ciphers (which use confusion) and block ciphers (which use diffusion.)

A reminder on ECB and CBC

Because block ciphers operate on blocks of data, it’s natural to chunk the plaintext into blocks, and encrypt each block independently. This mode of operation is called “Electronic Code Book” (ECB) and leads to catastrophic problems, because the same block of plaintext encrypted multiple times yields the same block of ciphertext! Summarized with this famous picture:

The fix for this is a new block encryption “mode”: Cipher-Block Chaining (CBC), where blocks of data to encrypt are XOR’d with the previous block ciphertext before being encrypted (for the first block to encrypt, it’s XOR’d with a public Initialization Vector because there is no previous ciphertext to use).

I found the explanation in the book crystal clear, and a nice reminder (or primer, if you have not seen this before!) on why block cipher modes are so important to get right.

Padding oracle attack

Another term widely used in the security industry, and explained well in the book. What it boils down to: an attacker shouldn’t be able to differentiate between a decryption operation which fails because the padding is incorrect vs. a complete failure to decrypt.

This “one bit” of information is enough to crack a ciphertext byte by byte:

• Take a ciphertext you know is valid.
• Work block by block, starting at the end.
• For each byte in a block, brute force one byte at a time: try all 256 values until there is no padding error.

This is a good reminder that if you’re working with sensitive workloads, granular error messages or error codes can lead to catastrophic consequences by leaking information to attackers.

BEAST explained

Another real-world exploit explained and implemented end-to-end: BEAST (stands for “Browser Exploit Against SSL/TLS”). I highly recommend reading this chapter (section 5.5) and the associated code. I wouldn’t do it justice by trying to explain it here, but it’s impressive that the authors managed to fit a full explanation and implementation for this exploit into a book chapter. I’ll leave you with a teaser: below is the diagram they work towards:

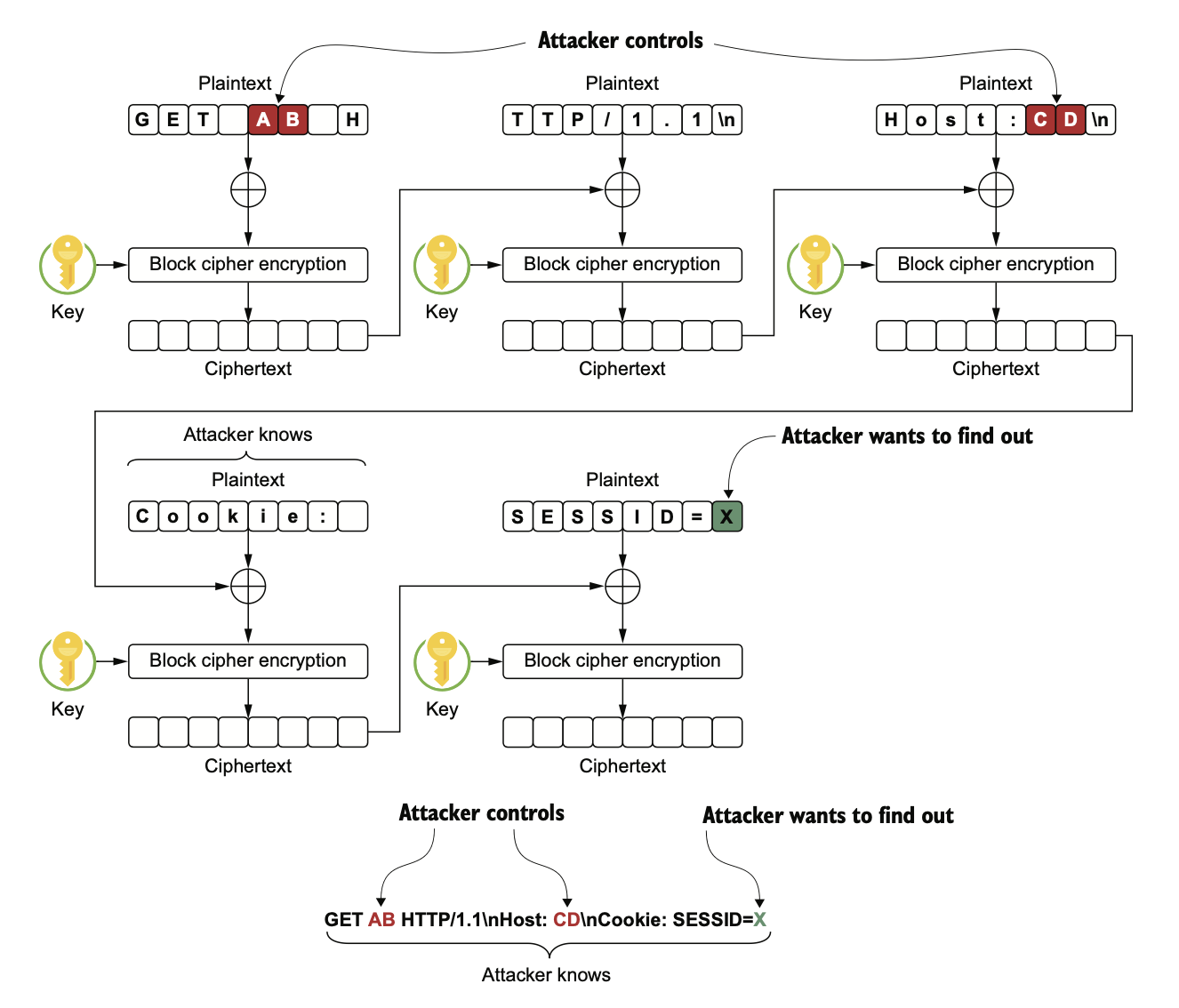
True beast of a diagram.

Birthday paradox and rainbow tables

Chapter 6 of the book covers a topic that’s well-covered everywhere: hash functions. Two concepts that are worth drilling home:

Birthday paradox

It takes a lot fewer people than you’d think to arrive at a group of people with at least one pair of people sharing a birthday. The parallel with hash functions is clear: it takes a lot fewer tries than you’d think for any one pair of inputs to share the same digest.

For a hash function producing digests which are of length N bits, there are `2^N` possible digest values, but it only takes `2^{N/2}` attempts to reach a 50% chance of generating a hash collision. More about the birthday paradox here, and more about collision resistance here.

Rainbow tables

I was under the impression that rainbow tables were simple key-value stores with digests as keys and passwords as values to allow attackers to reverse hash functions (and go from a stolen password digest to the actual password).

This isn’t true: rainbow tables are an optimization on top of this naive “simple lookup” approach. Rainbow tables rely on hash chains which alternate between applying a hash function and a reduce function, which goes from a digest value back to a candidate password deterministically. The optimization lies in the fact that a rainbow table only needs to store the start and the end of each hash chain, instead of storing all the intermediate digest values. How would lookups work for digests which are not stored, you say? That’s where the trick is. The lookup function isn’t a single DB lookup — it involves multiple lookups and computation:

• lookup a target digest value
• if not found, lookup digest2=hash(reduce(digest))
• if not found, lookup digest3=hash(reduce(digest2))
• …and so on until you’ve done this N times, where N is the length of the hash chain. If nothing is returned by that point, then the lookup has failed.

This is a clever way to trade-off space for time complexity. The book also explains why reduce functions must be indexed so that they’re different for each successive reduce operation: it avoids hash chains merging together. The result is the following diagram, which is a great, concise visual to remember why rainbow tables are called “rainbow tables”:

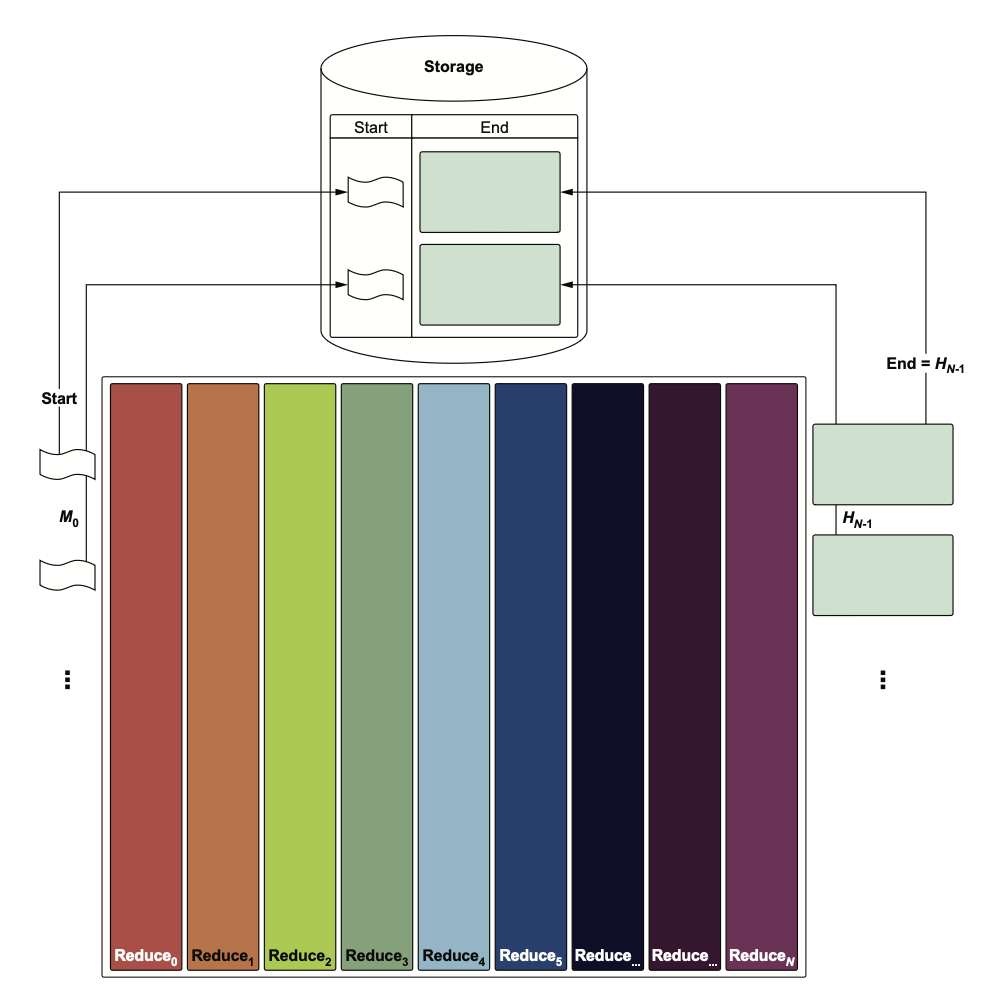
No way to un-see this once it clicks!

Just use HMAC

The book explains in detail how different types of Message Authentication Codes (MACs) fail:

• Secret-prefix MACs (where MAC = hash(secret || message)) are vulnerable to length-extension attacks. Length-extension attacks work on hash functions which use the Merkle–Damgård construction. In short, an attacker can construct H(A||B) from H(A) alone, without knowing A!
• Secret-suffix MACs (where MAC = hash(message || secret) aren’t vulnerable to length-extension attacks but vulnerable to collision attacks.

The solution: when you need a MAC, use HMAC. It fixes both problems.

Common factors attack on RSA

Something I learned while reading this book: there was an at-scale compromise of many RSA keys because they were not generated with good-enough entropy. This reminds me of Milksad, a vulnerability caused by weak entropy during crypto key generation.

The original paper is worth a read. If you’re looking for an implementation of the exploit, head here.

Small exponent attack (Wiener’s)

Mind-blowing attack because it relies on a mathematical theorem: Wiener’s Theorem. Exponents which are smaller than a threshold are vulnerable — there’s nothing anyone can do about it. That’s beautiful and scary at the same time: makes you wonder how much we truly know about the current crypto systems in use today. How many Wiener-style attacks exist but are currently unknown?

The book implements it fully: see the code for yourself here, it’s less than 50 lines.

RSA fixed points

Another lightbulb moment: I didn’t know RSA had fixed points. A fixed point is a plaintext which, when encrypted, yields itself. This seems like a serious bug to me! Here’s a visual for RSA fixed points:

From the book: “every RSA keypair has at least nine of them”. I found this surprising! The main defense against fixed points is randomized padding schemes, to make the odds of ending up on a fixed point negligible. But it doesn’t eliminate the possibility, it just makes it very small!

Nonce-reuse attacks

For readers who have not seen a nonce-reuse attack in action yet I highly recommend diving into the details of the math. It’s simple linear algebra. Reusing a nonce leads to full private key compromise, period.

This might break your mental model: if you think avoiding theft of your private key is enough to keep it safe…think again: If you’re tricked into using your private key to sign 2 different messages with the same nonce, your private key is gone. Whoops. This is what happened recently in this elliptic library vulnerability. Stay tuned, I’ll write about that more in the near future.

The defense against this is deterministic nonces (RFC 6979), or even better, hedged signatures.

Conclusion

Hacking Cryptography sits in that rare category of books that manage to make theory feel alive. It doesn’t just tell you that cryptography can fail; it shows you why, and it shows you how. Summary of what stuck with me deeply:

• True randomness comes from messy physics, and the best TRNGs are those with a clear, testable physical model like MEM-based designs. Without an underlying physical model, you can’t measure or trust your source of randomness.
• Even “true” random sources need mathematical cleanup to produce uniform, high-entropy output! Randomness extractors must be used on top of physical entropy sources.
• CSPRNGs vs. PRNGs: the line between “secure” and “insecure” PRNGs isn’t about randomness itself, but about how the underlying “next state” and “next output” functions are secure against inversion.
• The DUAL_EC_BG exploit is a very elegant backdoor, courtesy of our friends at the NSA. You have to know the backdoor to prove that there is a backdoor. We still do not know whether DUAL_EC_BG is actually backdoor’d, to this day.
• Stream ciphers are a practical solution to the limitation of One-Time Pads when the amount of data to encrypt grows larger and larger.
• WEP is insecure because of the underlying statistical bias in RC4. Incredible find and exploit.
• Padding oracle attacks are a good reminder that error messages, if they leak just one bit too much information, can lead to catastrophic consequences.
• Need a MAC? Just use HMAC.
• Pure math can be a sharp weapon: Wiener’s attack on small RSA exponents is a masterclass.
• Every RSA keypair has at least nine fixed points.
• Preventing key theft isn’t enough to protect your private key — nonce reuse can reveal it entirely. All that’s needed are two public signatures sharing the same nonce.

If you already work with crypto, this book will give you new mental models and sharpen your intuition for what can go wrong. If you’re new to the field, it will give you a practical foundation rooted in real attacks rather than abstract concepts.

I came away from it with a renewed appreciation for simplicity, paranoia, and humility when dealing with cryptography.

Thanks for reading!